Multiple Choice
Identify the
letter of the choice that best completes the statement or answers the question.
|
|
|
1.
|
You want to compute a 96% confidence interval for a
population mean. Assume that the population standard deviation is known to be 10 and the sample
size is 50. The critical value to be used in this calculation is
a. | 1.960 | b. | 1.645 | c. | 1.751 | d. | 2.054 | e. | None of the
above. |
|
|
|
2.
|
You have measured the systolic blood pressure of a
random sample of 25 employees of a company located near you. A 95% confidence interval for the
mean systolic blood pressure for the employees of this company is (122, 138). Which of the
following statements gives a valid interpretation of this interval?
a. | Ninety-five percent of the sample of employees have a
systolic blood pressure between 122 and 138. | b. | Ninety-five
percent of the population of employees have a systolic blood pressure between 122 and
138. | c. | If the procedure were repeated many times, 95% of the
resulting confidence intervals would contain the population mean systolic blood
pressure. | d. | The probability that the population mean blood pressure
is between 122 and 138 is 0.95. | e. | If the procedure
were repeated many times, 95% of the sample means would be between 122 and
138. |
|
|
|
3.
|
An analyst, using a random sample of n = 500
families, obtained a 90% confidence interval for mean monthly family income for a large population:
($600, $800). If the analyst had used a 99% confidence level instead, the confidence interval would
be:
a. | Narrower and would involve a larger risk of being
incorrect | b. | Wider and would involve a smaller risk of being
incorrect | c. | Narrower and would involve a smaller risk of being
incorrect | d. | Wider and would involve a larger risk of being
incorrect | e. | Wider but it cannot be determined whether the risk of
being incorrect would be larger or smaller |
|
|
|
4.
|
In an opinion poll, 25% of a random sample of 200
people said that they were strongly opposed to having a state lottery. The standard error of
the sample proportion is approximately
a. | 0.03 | b. | 0.25 | c. | 0.0094 | d. | 6.12 | e. | 0.06 |
|
|
|
5.
|
In preparing to use a t procedure, suppose
we were not sure if the population was Normal. In which of the following circumstances would we
not be safe using a t procedure?
a. | A stemplot of the data is roughly
bell-shaped. | b. | A histogram of the
data shows moderate skewness. | c. | A stemplot of the
data has a large outlier. | d. | The sample
standard deviation is large. | e. | The t
procedures are robust, so it is always safe. |
|
|
|
6.
|
In a poll, (a) some people refused to answer
questions, (b) people without telephones could not be in the sample, and (c) some people never
answered the phone in several calls. Which of these sources is included in the ±2% margin
of error announced for the poll?
a. | Only source (a). | b. | Only source (b). | c. | Only source
(c). | d. | All three sources of error. | e. | None of these sources of error. |
|
|
|
7.
|
You want to compute a 90% confidence interval for
the mean of a population with unknown population standard deviation. The sample size is
30. The value of t* you would use for this interval is
a. | 1.96 | b. | 1.645 | c. | 1.699 | d. | 0.90 | e. | 1.311 |
|
|
|
8.
|
The college newspaper of a large Midwestern
university periodically conducts a survey of students on campus to determine the attitude on campus
concerning issues of interest. Pictures of the students interviewed along with quotes of their
responses are printed in the paper. Students are interviewed by a reporter
“roaming” the campus selecting students to interview “haphazardly.” On
a particular day the reporter interviews five students and asks them if they feel there is adequate
student parking on campus. Four of the students say, “no.” Which of the following
conditions for inference about a proportion using a confidence interval are violated in this
example?
a. | The data are an SRS from the population of
interest. | b. | The population is at least ten times as large as the
sample. | c. | 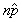 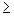 10 and 10 and 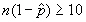 . . | d. | We are interested
in inference about a proportion. | e. | More than one
condition is violated. |
|
|
|
9.
|
To assess the accuracy of a laboratory scale, a
standard weight that is known to weigh 1 gram is repeatedly weighed a total of n times and the
mean 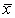 of the weighings is computed. Suppose the scale readings are Normally distributed with
unknown mean of the weighings is computed. Suppose the scale readings are Normally distributed with
unknown mean 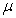 and standard deviation and standard deviation 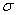 = 0.01 g. How large
should n be so that a 95% confidence interval for = 0.01 g. How large
should n be so that a 95% confidence interval for 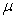 has a margin of error of ±
0.0001? has a margin of error of ±
0.0001?
a. | 100 | b. | 196 | c. | 27,061 | d. | 10,000 | e. | 38,416 |
|
|
|
10.
|
Many television viewers express doubts about the
validity of certain commercials. In an attempt to answer their critics, the Timex Corporation
wishes to estimate the proportion of consumers who believe what is shown in Timex television
commercials. Let p represent the true proportion of consumers who believe what is shown
in Timex television commercials. If Timex has no prior information regarding the true value of
p, how many consumers should be included in their sample so that they will be 95% confident
that their estimate is within 0.03 of the true value of p?
a. | 202 | b. | 203 | c. | 1067 | d. | 1068 | e. | 1165 |
|