Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Suppose we have two SRSs from two distinct
populations and the samples are independent. We measure the same variable for both
samples. Suppose both populations of the values of these variables are Normally distributed but
the population means and standard deviations are unknown. For purposes of comparing the two
means, we use
A) | Two-sample t
procedures | B) | Matched pairs
t procedures | C) | Two-proportion
z procedures | D) | The least-squares
regression line | E) | None of the
above. |
|
|
|
2.
|
We wish to test if a new feed increases the mean
weight gain compared to an old feed. At the conclusion of the experiment it was found that the new
feed gave a 10 kg bigger gain than the old feed. A two-sample t test with the proper one-sided
alternative was done and the resulting P-value was 0.082. This means that
A) | there is an 8.2% chance the null hypothesis is
true. | B) | there was only an 8.2% chance of observing an increase
greater than 10 kg (assuming the null hypothesis was true). | C) | there was only an 8.2% chance of observing an increase greater than 10 kg
(assuming the null hypothesis was false). | D) | there is an 8.2%
chance the alternative hypothesis is true. | E) | there is only an
8.2% chance of getting a 10 kg increase. |
|
|
|
3.
|
A study was conducted to investigate the
effectiveness of a new drug for treating Stage 4 AIDS patients. A group of AIDS patients was randomly
divided into two groups. One group received the new drug; the other group received a placebo. The
difference in mean subsequent survival (those with drugs – those without drugs) was found to be
1.04 years, and a 95% confidence interval was found to be 1.04 ± 2.37 years. Based upon this
information, we can conclude that
A) | the drug was effective since those taking the drug
lived, on average, 1.04 years longer. | B) | the drug was
ineffective since those taking the drug lived, on average, 1.04 years
less. | C) | there is no evidence the drug was effective since the
95% confidence interval covers zero. | D) | there is evidence
the drug was effective since the 95% confidence interval does not cover
zero. | E) | we can make no conclusions since we do not know the
sample size or the actual mean survival of each group. |
|
|
|
4.
|
Different varieties of fruits and vegetables have
different amounts of nutrients. These differences are important when these products are used to make
baby food. We wish to compare the carbohydrate content of two varieties of peaches. Specifically, we
wish to test if the two varieties are significantly different in their mean carbohydrate content. The
null and alternative hypotheses are
|
|
|
5.
|
Thirty-five people from a random sample of 125
workers from Company A admitted to using sick leave when they weren’t really ill.
Seventeen employees from a random sample of 68 workers from Company B admitted that they had used
sick leave when they weren’t ill. A 90% confidence interval for the difference in the
proportions of workers at the two companies who would admit to using sick leave when they
weren’t ill is
|
|
|
6.
|
To use the two-sample t procedure to perform
a significance test on the difference between two means, we assume that
A) | the populations’ standard deviations are
known. | B) | the samples from each population are
independent. | C) | the distributions
are exactly Normal in each population. | D) | the sample sizes
are large. | E) | all of the
above |
|
|
|
7.
|
In a large midwestern university (the class of
entering freshmen being on the order of 6000 or more students), an SRS of 100 entering freshmen in
1993 found that 20 finished in the bottom third of their high school class. Admission standards
at the university were tightened in 1995. In 1997 an SRS of 100 entering freshmen found that 10
finished in the bottom third of their high school class. Let p1 and
p2 be the proportion of all entering freshmen in 1993 and 1997, respectively, who
graduated in the bottom third of their high school class. What conclusion should we
draw?
A) | We are 95% confident that the admissions standards have
been tightened. | B) | Reject
H0 at the 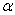 = 0.01 significance
level. = 0.01 significance
level. | C) | Fail to reject H0 at the 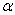 = 0.05 significance level. = 0.05 significance level. | D) | There is
significant evidence at the 5% level of a decrease in the proportion of freshmen who graduated in the
bottom third of their high school class that were admitted by the
university. | E) | If we reject
H0 at the 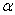 = 0.05 significance level based on these results, we
have a 5% chance = 0.05 significance level based on these results, we
have a 5% chance
of being
wrong. |
|
|
|
8.
|
42 of 65 randomly selected people at a baseball
game report owning an iPod. 34 of 52 randomly selected people at a rock concert occurring at
the same time across town reported owning an iPod. A researcher wants to test the claim that
the proportion of iPod owners at the two venues is not the same. A 90% confidence interval for
the difference in population proportions is 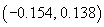 . Which of the following
gives the correct outcome of the researchers’ test of the claim? . Which of the following
gives the correct outcome of the researchers’ test of the claim?
A) | Since the confidence interval includes 0, the researcher
can conclude that the proportion of iPod owners at the two venues is the
same. | B) | Since the confidence interval includes 0, the researcher
can conclude that the proportion of iPod owners at the two venues may be the
same. | C) | Since the confidence interval includes 0, the researcher
can conclude that the proportion of iPod owners at the two venues is
different. | D) | Since the
confidence interval includes more positive than negative values, we can conclude that a higher
proportion of people at the baseball game own iPods than at the rock
concert. | E) | We cannot draw a conclusion about a claim without
performing a significance test. |
|
|
|
9.
|
The power takeoff driveline on tractors used in
agriculture is a potentially serious hazard to operators of farm equipment. The driveline is covered
by a shield in new tractors, but for a variety of reasons, the shield is often missing on older
tractors. Two types of shields are the bolt-on and the flip-up. It was believed that the bolt-on
shield was perceived as a nuisance by the operators and deliberately removed, but the flip-up shield
is easily lifted for inspection and maintenance and may be left in place. In a study initiated by the
U.S. National Safety Council, a sample of older tractors with both types of shields was taken to see
what proportion were removed. Of 183 tractors designed to have bolt-on shields, 35 had been removed.
Of the 136 tractors with flip-up shields, 15 were removed. We wish to test the hypothesis
H0: pb = pf vs. Ha:
pb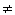 pf where pb and
pf are the proportion of tractors with the bolt-on and flip-up shields removed,
respectively. Which of the following conditions for performing the appropriate significance
test is satisfied in this case? pf where pb and
pf are the proportion of tractors with the bolt-on and flip-up shields removed,
respectively. Which of the following conditions for performing the appropriate significance
test is satisfied in this case?
A) | Both population distributions are Normally
distributed. | B) | Two independent
simple random samples were chosen. | C) | Both sample sizes
are at least 30. | D) | np and
n(1 – p) are both large enough to use Normal
calculations. | E) | The sample size is
at least 10 times the population size. |
|
|
|
10.
|
All of us nonsmokers can rejoice—the mosaic
tobacco virus that affects and injures tobacco plants is spreading! Meanwhile, a tobacco company is
investigating if a new treatment is effective in reducing the damage caused by the virus. Eleven
plants were randomly chosen. On each plant, one leaf was randomly selected, and one half of the leaf
(randomly chosen) was coated with the treatment, while the other half was left untouched (control).
After two weeks, the amount of damage to each half of the leaf was assessed.
What is the best reason for performing a paired experiment rather than a
two–independent sample experiment in this case?
A) | It is easier to do since we need fewer experimental
units and each unit receives more than one treatment. | B) | It allows us to remove variation in the results caused by other factors since
we can compare both treatments within the same experimental unit. | C) | The computer program is more accurate since we work only with the
differences. | D) | It requires fewer
assumptions since we are interested only in the difference between
treatments. | E) | It allows us to do
more experiments since we use each experimental unit twice. |
|