Multiple Choice
Identify the
choice that best completes the statement or answers the question.
|
|
|
1.
|
Following a dramatic drop of 500 points in the Dow
Jones Industrial Average in September 1998, a poll conducted for the Associated Press found that 92%
of those polled said that a year from now their family financial situation will be as good as it is
today or better. The number 92% is a
a. | Statistic | b. | Sample | c. | Parameter | d. | Population | e. | None of the
above. |
|
|
|
2.
|
In a large population, 46% of the households own
VCR’s. A simple random sample of 100 households is to be contacted and the sample
proportion computed. The mean of the sampling distribution of the sample proportion
is
a. | 46 | b. | 0.46 | c. | About 0.46, but
not exactly 0.46 | d. | 0.00248 | e. | The answer cannot
be computed from the information given |
|
|
|
3.
|
If a population has a standard deviation 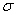 , then the standard deviation of the mean of 100 randomly selected items from this
population is , then the standard deviation of the mean of 100 randomly selected items from this
population is
a. | 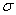 |
b. | 100 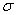 |
c. | 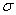 /10 /10 |
d. | 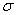 /100 /100 |
e. | 0.1 |
|
|
|
4.
|
A statistic is said to be unbiased
if
a. | The survey used to obtain the statistic was designed so
as to avoid even the hint of racial or sexual prejudice | b. | The mean of its sampling distribution is equal to the true value of the
parameter being estimated | c. | Both the person
who calculated the statistic and the subjects whose responses make up the statistic were
truthful | d. | It is used for honest purposes
only | e. | None of the
above. |
|
|
|
5.
|
The number of undergraduates at Johns Hopkins
University is approximately 2000, while the number at Ohio State University is approximately
40,000. At both schools a simple random sample of about 3% of the undergraduates is
taken. Which of the following is the best conclusion?
a. | The sample from Johns Hopkins has less sampling
variability than that from Ohio State. | b. | The sample from
Johns Hopkins has more sampling variability than that from Ohio State. | c. | The sample from Johns Hopkins has almost the same sampling variability as that
from Ohio State. | d. | It is impossible
to make any statement about the sampling variability of the two samples since the students surveyed
were different. | e. | None of the
above. |
|
|
|
6.
|
In a large population, 46% of the households own
VCRs. A simple random sample of 100 households is to be contacted and the sample proportion
computed. What is the standard deviation of the sampling distribution of the sample
proportion?
a. | 46 | b. | 0.46 | c. | 0.00248 | d. | 0.005 | e. | None of the
above. |
|
|
|
7.
|
In a large population of adults, the mean IQ is 112
with a standard deviation of 20. Suppose 200 adults are randomly selected for a market research
campaign. The distribution of the sample mean IQ is
a. | Exactly normal, mean 112, standard deviation
20. | b. | Approximately normal, mean 112, standard deviation
0.1. | c. | Approximately normal, mean 112, standard deviation
1.414. | d. | Approximately normal, mean 112, standard deviation
20. | e. | Exactly normal, mean 112, standard deviation
1.414. |
|
|
|
8.
|
Suppose we are planning on taking an SRS from a
population. If we double the sample size, then 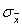 will be multiplied by: will be multiplied by:
|
|
|
A factory produces plate glass with a mean
thickness of 4 millimeters and a standard deviation of 1.1 millimeters. A simple random sample of 100
sheets of glass is to be measured, and the sample mean thickness of the 100 sheets 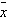 is to be computed.
is to be computed.
|
|
|
9.
|
We know the random variable 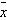 has
approximately a normal distribution because of has
approximately a normal distribution because of
a. | the law of large numbers. | b. | the central limit theorem. | c. | the law of proportions. | d. | the fact that
probability is the long run proportion of times an event
occurs. |
|
|
|
10.
|
The probability that the average thickness 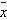 of the 100 sheets of glass is less than 4.1 millimeters is
approximately of the 100 sheets of glass is less than 4.1 millimeters is
approximately
a. | 0.8186. | c. | 0.1814. | b. | 0.3183. | d. | 0.6817. |
|